Compléments d'analyse S6 - Quelques compléments aux compléments

Quelques livres:

• Sur l'intégration:

  • Axler, Measure, Integration and Real Analysis, (MIRA pour les intimes - en anglais, mais vraiment agréable à lire).

  • Une référence en français: l'excellent polycopié de Thierry Gallay, disponible ici.
  • Une autre référence, très complète: Analyse - Théorie de l'intégration de Gilles Pagès et Marc Briane, disponible à la bibliothèque.
  • De l'intégration aux probabilités, par Olivier Garet et Aline Kurtzmann.
  • Pour s'entraîner: Exercices corrigés en théorie de la mesure et intégration, de Jean-Pascal Ansel et Yves Ducel.
• Sur le calcul différentiel
  • Petit guide de calcul différentiel, de François Rouvière : Résumé de cours et exercices - assez avancés, mais entièrement corrigés, ils permettent d'approfondir la compréhension (et le goût !) pour le calcul différentiel
  • A First Course in Optimization Theory, de Rangarajan K. Sundaram, pour la partie optimisation.

Quelques documents

Cours

• Chapitre 0 : Rappels de calcul différentiel
• Chapitre 1 : Inversion locale et fonctions implicites
• Chapitre 2 : Extrema liés
• Chapitre 3 : Espaces $L^p$
• Chapitre 4: L'espace hilbertien $L^2$

Exercices

• Rappels de calcul différentiel
• Rappels de calcul intégral
• Théorèmes d'inversion locale et des fonctions implicites
• Théorème des extrema liés
• Espaces $L^p$
• Espace $L^2$

Quelques fiches de synthèse

• Calcul différentiel - définitions
• Calcul différentiel - méthodes
• Théorie de la mesure et intégration de Lebesgue

Quelques suppléments:

• Preuve du Théorème d'inversion locale: Régularité de l'inverse
• Preuve du théorème des fonctions implicites
• Théorème des extrema liés à plusieurs contraintes
• Quelques applications du TFI en optimisation
• De la théorie de la mesure aux probabilités: une petite traduction
• Construction des espaces $L^p$
• Un ensemble Lebesgue-mesurable qui n'est pas borélien
• Un ensemble non Lebesgue-mesurable
• Comparaison des intégrales de Lebesgue et de Riemann
• De la tribu de Borel à celle de Lebesgue
• Intégrale de Stieltjes

Première partie: Intégration et espaces de Lebesgue

Résumé des épisodes précédents

Un résumé de théorie de la mesure et intégration à la Lebesgue est disponible sur la page d'intégration.

Et pour plus de détails sur la théorie de la mesure, voir ici.

Enfin, vous trouverez ici des exemples de tribus, de mesures, d'ensembles négligeables et d'ensembles bizarres.

Enfin, vous trouverez ci-dessous quelques portraits de suites de fonctions sauvages et qui refusent de passer à la limite dans les intégrales, sur l'excellent site Math3ma:

• Une suite qui converge presque partout, mais dont l'intégrale ne converge pas
• Une suite qui converge uniformément, mais pas en norme intégrale
• Une suite de fonctions toutes intégrables, convergeant uniformément vers une limite non intégrable
• Une suite qui converge simplement (point par point), mais pas en norme intégrale
• Une suite dont les intégrales convergent, mais qui ne converge en aucun point.

Espaces de Lebesgue

Dans ce cours de compléments, on va s'intéresser à une certaine catégories d'espaces fonctionnels (c'est-à-dire d'espaces vectoriels normés dont les éléments sont des fonctions), définis à partir d'intégrales.

Pourquoi faire ? L'idée de l'analyse fonctionnelle est de décrire de tels espaces vectoriels, de façon à pouvoir étudier des questions sur les fonctions en termes d'algèbre linéaire et de topologie sur les espaces vectoriels normés.

Ainsi, on peut aborder la résolution d'une équation aux dérivées partielles, par exemple $$ \frac{\partial u}{\partial t} = k\frac{\partial^2 u}{\partial x^2} $$ en se demandant: pour quel choix de norme sur les espaces vectoriels $\mathcal C^2(\mathbb R^2,\mathbb{R})$ et $\mathcal C^0(\mathbb R^2,\mathbb{R})$ l'application linéaire $D: u\in\mathcal C^2(\mathbb R^2,\mathbb{R}) \mapsto \frac{\partial u}{\partial t} - \frac{\partial^2 u}{\partial x^2}\in \mathcal C^0(\mathbb R^2,\mathbb{R})$ est-elle continue ?

Ou encore, quelles sont les valeurs propres de l'application linéaire $u\mapsto \frac{\partial^2 u}{\partial x^2}$ ? Peut-on décomposer toute fonction comme somme de vecteurs propres ?

Dans le cadre de l'analyse fonctionnelle, les espaces vectoriels qui nous intéressent sont de dimension infinie, donc toutes les normes n'y sont pas équivalentes: d'où l'intérêt de choisir "la bonne norme" pour étudier un problème donné.

Pour pouvoir utiliser les plus puissants théorèmes sur les e.v.n., comme par exemple le théorème du point fixe, une des conditions essentielle est la complétude de l'espace vectoriel. Sur un espace vectoriel $E$, on va donc particulièrement rechercher des normes telles que l'e.v.n. $(E,\|.\|)$ soit un espace de Banach.

Un exemple de cette idée ici: deux normes sur $\mathcal C^0$.

C'est encore mieux si la norme est obtenue à partir d'un produit scalaire sur $E$, car on dispose alors des notions d'endomorphismes autoadjoints (qui sont diagonalisables en dimension finie, et demeurent sympathiques en dimension infinie) et surtout de projection orthogonale. Un espace euclidien complet $(E, \langle .,.\rangle)$ est appelé un espace de Hilbert.

Et donc, les espaces de Lebesgue: vous connaissez déjà l'ensemble $\mathscr L^0$ des fonctions réelles mesurables, ainsi que l'ensemble $\mathscr L^1$ des fonctions intégrables, c'est-à dire telles que $$\int_{\mathbb R} |f| d\lambda < \infty$$
Pour $p>1$, on va s'intéresser à l'ensemble $$ \mathscr L^p=\{f\in \mathscr L^0, \int_\mathbb{R} |f|^p d\lambda < \infty\} $$ sur lequel on peut donc définir une "norme" $$ \|f\|_p = \left(\int_\mathbb{R} |f|^p d\lambda\right)^\frac1p $$

Pourquoi les guillemets ? $\|.\|_p$ n'est pas tout à fait une norme sur $\mathscr L^p$: il existe des fonctions, nulles Lebesgue-presque partout, telles que $\|f\|_p=0$ mais $f\neq 0$.

On peut contourner ce problème par un procédé de passage au quotient, qui nous donne un ensemble $L^p$ sur lequel $\|.\|_p$ est une vraie norme. De plus, ce sont des espaces de Banach: les $(L^p,\|.\|_p)$ sont appelés espaces de Lebesgue.

Et encore mieux, $L^2$, muni du produit scalaire $$\langle f,g\rangle = \int_\mathbb R fg d\lambda$$ est un espace de Hilbert.

Deuxième partie: Inversion locale et fonctions implicites

Il ne vous aura pas échappé que, quand il s'agit d'étudier des fonctions, la dérivée, et sa généralisation aux e.v.n.: la différentielle, sont des outils indispensables.

Vous trouverez quelques rafraîchissements là-dessus sur cette page. En un mot:

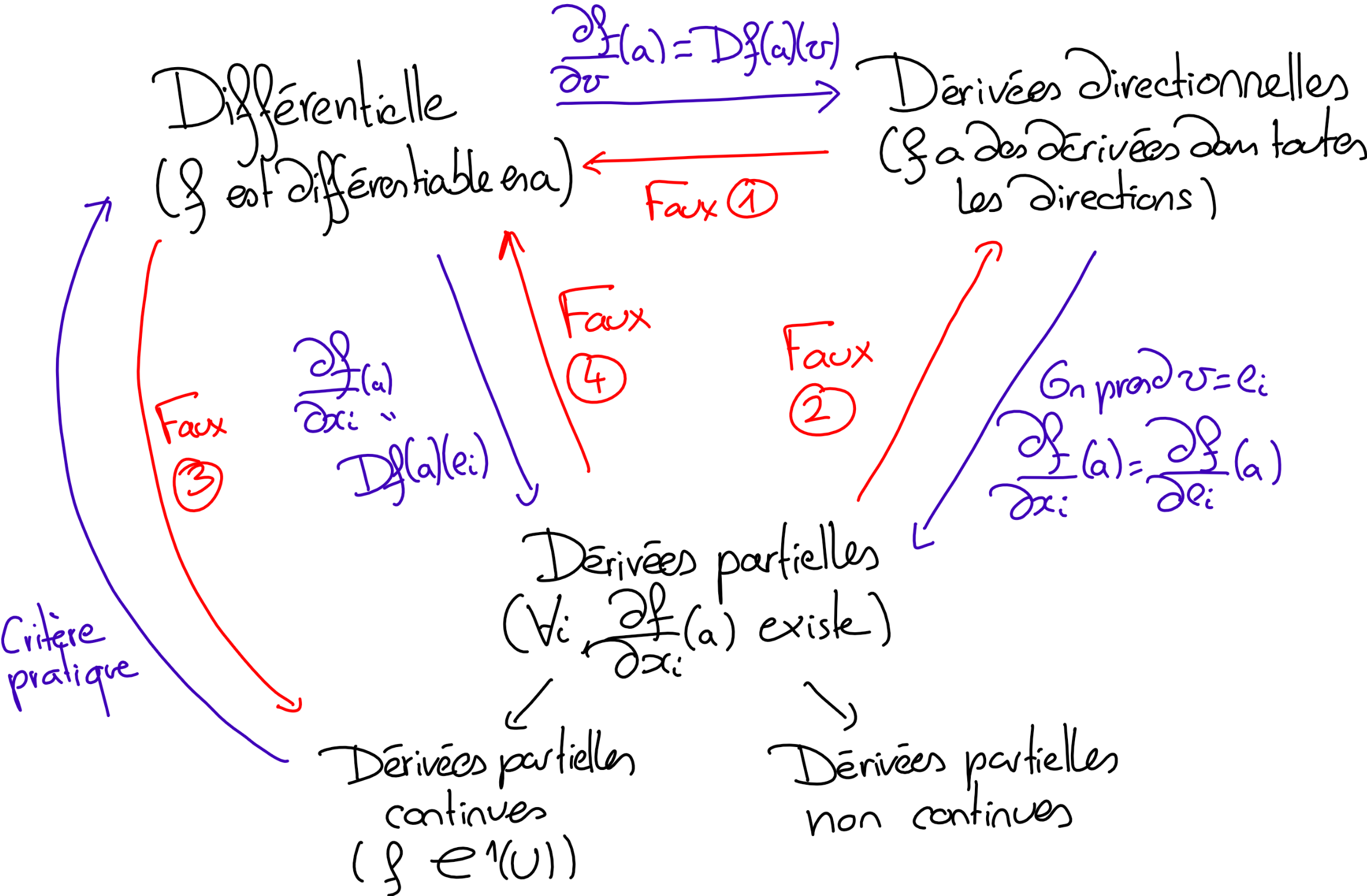
Les contre-exemples 1,2,3 et 4 du diagramme sont explicités ici.

On l'a dit, la Grande Idée du Calcul Différentiel, c'est que l'algèbre linéaire c'est super. Donc, on essaie d'approximer localement nos fonctions par une application linéaire, qu'on appelle la différentielle.

La question qu'on va se poser ici, c'est comment cette idée peut aider à résoudre des équations.

Ainsi, si on prend un système (non linéaire) à $p$ équations, d'inconnue $x\in \mathbb R^n$ $$ \begin{cases} f_1(x_1,\ldots,x_n)&=u_1\\ \vdots\\ f_p(x_1,\ldots,x_n)&=u_p \end{cases} $$ et si $f$ est différentiable, alors on peut se ramener localement à un système linéaire. Et ça, on sait résoudre:

• il y a une unique solution si $n=p=$ rang du système
• il y a une infinité de solutions, décrites par des variables paramètres, si $n>p$.

Les deux grands théorèmes dont on va parler, le théorème d'Inversion Locale (TIL) et le théorème des Fonctions Implicites (TFI), précisent ce qu'on peut obtenir dans chacun de ces deux cas:

• Le Théorème d'Inversion Locale s'applique dans le cas $n=p$: à quelle condition peut-on "inverser" le système, c'est à dire résoudre $f(x)=u$ en $x=f^{-1}(u)$ ?
• Le Théorème des Fonctions Implicites s'applique dans le cas $n>p$: à quelle condition peut-on choisir des variables "paramètres" $z_{p+1},\ldots,z_n$ et résoudre $f(x,z)=0$ en $x=\psi(z)$ ?

Heuristique du TIL

Cas linéaire Soit $f:\mathbb R^n\rightarrow \mathbb R^p$ une application linéaire.
Alors l'équation $y=f(x)$ a une unique solution $x\in\mathbb R^n$ si, et seulement si, $n=p$ et si la matrice $A$ de $f$ dans la base canonique de $\mathbb R^n$ est inversible.

D'un point de vue différentiel, dans ce cas, pour tout $x\in \mathbb R^n$, $Df(x)=f$ et $Jac_f(x) = A$.

$\leadsto$ On a donc $f$ inversible ssi $Df(x)$ inversible.

Cas différentiable Soient $f:U\subset \mathbb R^n \rightarrow \mathbb R^n$ $\mathcal C^1$, $x_0\in U$ et $y_0=f(x_0)$.

On souhaite résoudre $f(x)=y$ pour $(x,y)$ proches de $(x_0,y_0)$. Posons donc $y=y_0+k$ et cherchons $x$ sous la forme $x_0+h$. Alors $f(x)=y$ se réécrit $f(x_0+h)=y_0+k$: $$ f(x_0)+ Df(x_0)(h) \simeq y_0+k=f(x_0)+k $$ donc, si $Df(x_0)$ est inversible, la solution est donnée par $$ \begin{align*} f^{-1}(y)& = x_0+h=x_0+Df(x_0)^{-1}(k)+\text{chouïa}\\ &= f^{-1}(y_0)+Df(x_0)^{-1}(y-y_0)+\text{chouïa} \end{align*} $$

Plus qu'à rigorifier tout ça !

Un contre-exemple si on suppose seulement que $f$ est dérivable, et non $\mathcal C^1$:

By Magyar25 - Own work, CC BY-SA 4.0, Link

Heuristique du TFI

Cas linéaire Considérons par exemple le système $$ (\mathcal S) \begin{cases} x+y+z&=0 \\ 2x+2y+z&=1 \end{cases} \iff \begin{cases} x+y+z&=0\\ \phantom{x+{}}x+y&=1 \end{cases} \iff \begin{cases} z&=-1\\ y&=1-x \end{cases} $$ $\leadsto$ L'ensemble des solutions de $(\mathcal S)$ est le graphe $\{(x,\varphi(x)),x\in\mathbb R\}$ de la fonction $\varphi:x\in \mathbb R \mapsto (1-x,-1)\in\mathbb R^2$.

En prime, pour savoir combien d'inconnues mettre en paramètre et lesquelles, on dispose de l'algorithme du pivot de Gauss, qui nous permet d'échelonner le système.

Quel est le bon critère pour faire ça quand les équations ne sont pas linéaires ?

Découpons la jacobienne. Pour $f$ une application $\mathcal C^1$ sur $\mathbb R^n=\mathbb R^{n-p} \times \mathbb R^p$: $$ \begin{align*} f:\mathbb R^{n-p} \times \mathbb R^p &\rightarrow \mathbb R^p \\ (x,y)&\mapsto f(x,y) \end{align*} $$ on décompose la jacobienne de $f$ en deux parties:

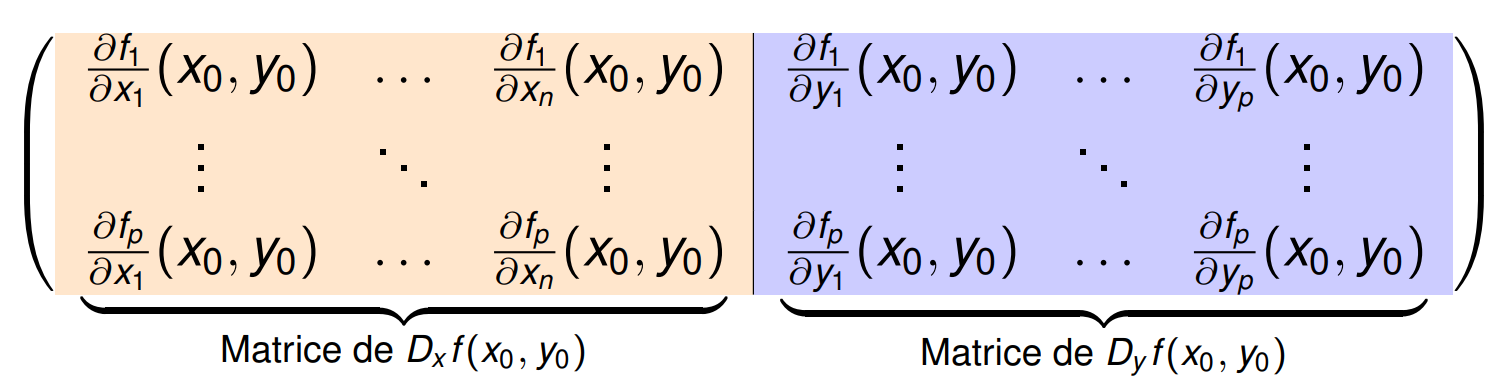
On a donc, pour $(h,k)\in \mathbb R^n\times \mathbb R^p$,

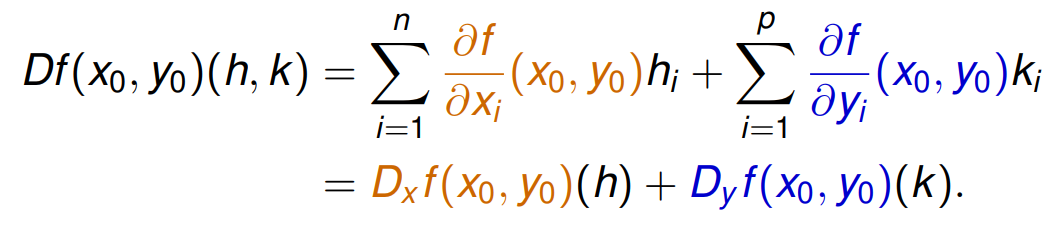
Supposons que $f(x_0,y_0)=0_{\mathbb R^p}$ et résolvons l'équation $f(x,y)=0$ près de $(x_0, y_0)$ en fonction de $x$.

Autrement dit on cherche $\varphi:V\subset\mathbb R^n\rightarrow\mathbb R^p$ telle que $$ f(x,y)=0 \iff y=\varphi(x). $$ Or, au voisinage de $(x_0,y_0)$, on a $$ \begin{align*} f(x,y)&=f(x_0,y_0)+Df(x_0,y_0)(x-x_0,y-y_0)+\text{chouïa}\\ &=D_xf(x_0,y_0)(x-x_0)+D_yf(x_0,y_0)(y-y_0)+\text{chouïa} \end{align*} $$ Donc l'équation $f(x,y)=0$ se réécrit $$ D_y f(x_0,y_0)(y-y_0)=-D_xf(x_0,y_0)(x-x_0)+\text{chouïa} $$

$\leadsto$ Si $D_yf(x_0,y_0)$ est inversible, il y a une unique solution $$ y=\varphi(x)=y_0-(D_y f(x_0,y_0)^{-1}D_xf(x_0,y_0))(x-x_0)+... $$

Un exemple: $f:(x,y)\in\mathbb R \times \mathbb R \mapsto x^2+y^2-1 \in \mathbb R$:

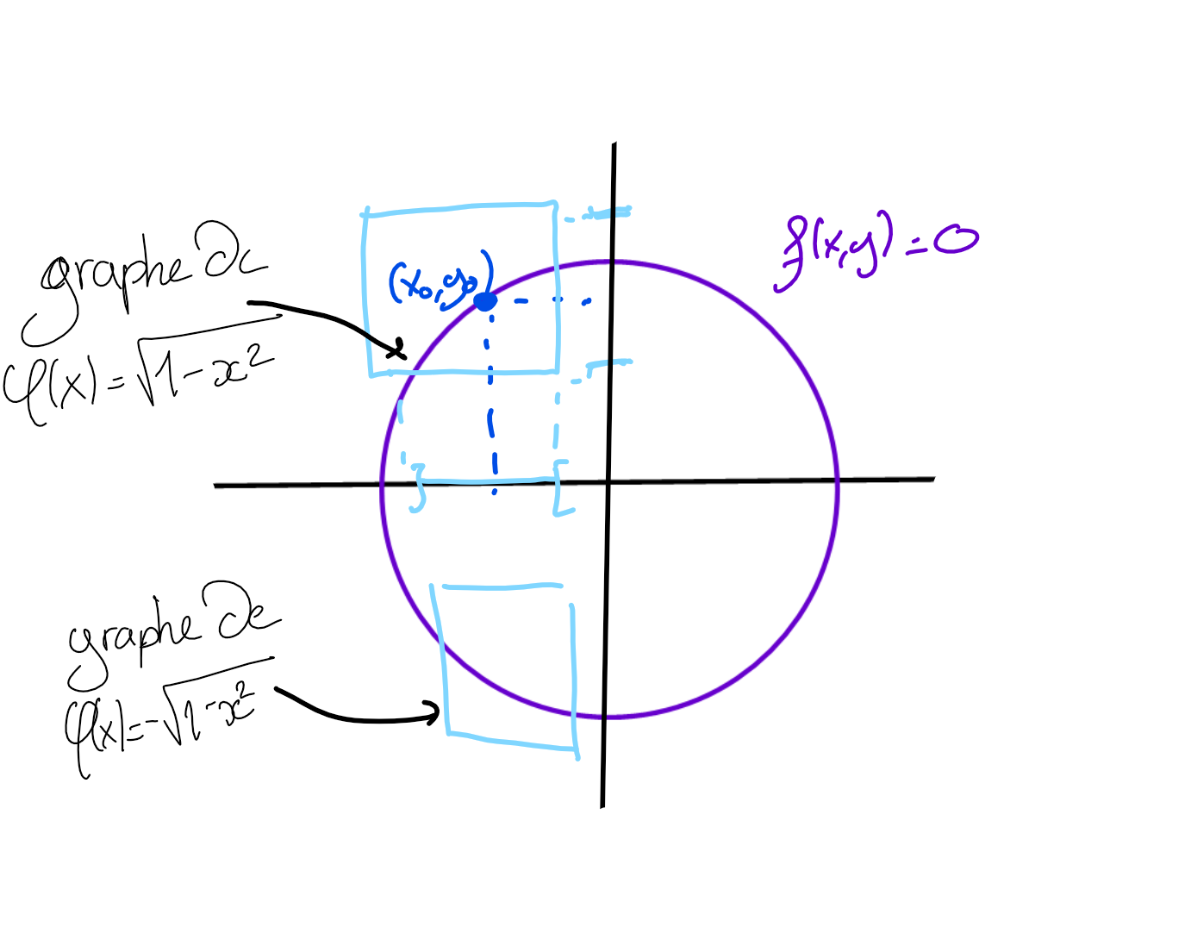
Plus qu'à rigorifier tout ça !

Sous-variétés

On peut pousser plus loin la Grande Idée du calcul différentiel, et s'intéresser à des espaces qui ne sont pas des espaces vectoriels, mais qui, localement, y ressemblent. Une sphère, par exemple: ce n'est pas un espace vectoriel, mais depuis la surface de la Terre, localement donc, on a quand même furieusement l'impression de marcher sur $\mathbb R^2$.

Etudier à quoi ressemblent de tels ensembles, ça s'appelle la géométrie différentielle. Une intro ici: