Analyse dans $\mathbb R^n$

By Ignacio Garcia - https://www.flickr.com/photos/am104//, CC BY 2.0, Link

Quelques références:

• Complément de cours: Liret, Martinais, Analyse L2, chapitres 5 et 6 (pour les espaces vectoriels normés.
• Fiches-méthodes: Merlin, MethodiX Analyse, chapitre 3 et 16. Voir aussi A.El Kaabouchi, D. Essayed, Mathématiques L2, chapitres 10 et 11.

Quelques aides-mémoires:

• Fiche récapitulative sur les espaces normés
• Fiche sur la compacité et la complétude dans les espaces normés
• Fiche méthode sur la continuité dans les espaces normés

Pourquoi analyser dans $\mathbb R^n$ ?

Lorsqu'on veut comprendre comment un phénomène dépend d'un autre, on se retrouve à étudier une fonction: comment le pouvoir d'achat évolue en fonction du chômage, par exemple. Et si on peut quantifier chacun des deux phénomènes, autrement dit le représenter par un nombre, on se retrouve plus spécifiquement avec une fonction $\mathbb R \rightarrow \mathbb R$.

Par GedefrTravail personnel, CC BY-SA 3.0, Lien

L'analyse réelle donne un assortiment d'outils pour extraire toute l'information d'une telle fonction: est-ce qu'elle augmente ? Est-ce qu'elle diminue ? Quelles sont ses valeurs maximales, minimales, et où sont-elles ?

Mais il se trouve que la plupart des phénomènes intéressants ne dépendent pas d'une seule cause, et ne sont donc pas entièrement décrits par des fonctions d'une seule variable. D'où l'intérêt de s'intéresser à des fonctions à plusieurs variables: autrement dit, des fonctions $\mathbb R^n\rightarrow \R^p.

Comment analyser dans $\mathbb R^n$ ?

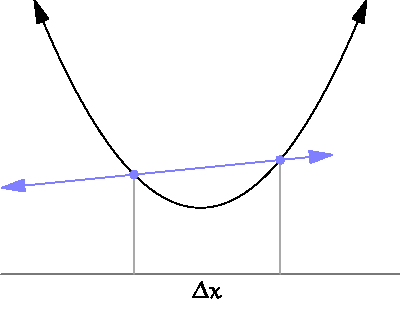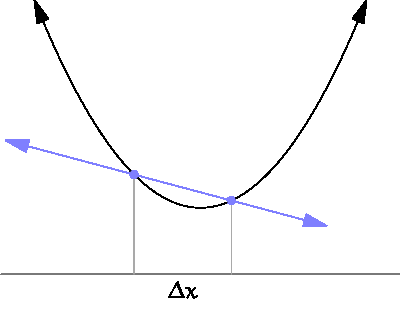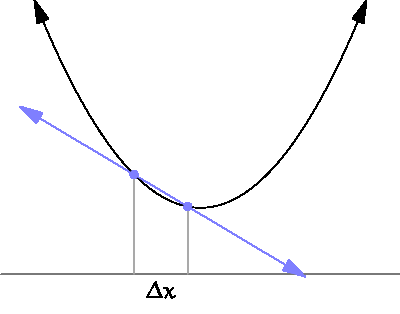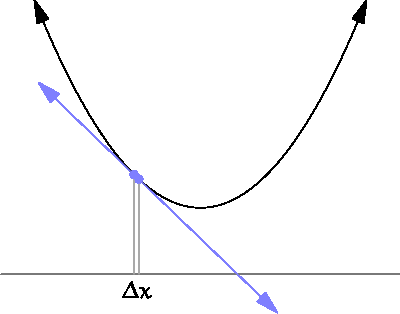
Continuité, dérivabilité, intégration... Une idée sous-tend tous les outils de l'analyse: on approxime la question par une question plus simple, puis on passe à la limite.

Ainsi, la dérivée, qui nous donne accès aux variations de la fonction, s'obtient en faisant une limite de taux d'accroissements; l'intégrale est une limite de somme d'aires de rectangles...

By Brnbrnz; - Own work, CC BY-SA 4.0, Link

By Lucas Vieira - Own work, Public Domain, Link

Autrement dit, en très très gros, il s'agit de voir de quoi se "rapproche" une quantité quand un point se "rapproche" d'un autre.
Donc en fin de compte, ce qui est au fondement de l'analyse, c'est la possibilité de mesurer la distance entre deux points.

Dans $\mathbb R$, on fait ça avec la valeur absolue: c'est pourquoi les définitions en analyse réelle ont cette tête là: $$ \begin{align*} \forall \varepsilon > 0,\ \exists \eta>0,\, |x-a|<\eta \Rightarrow |f(x)-f(a)|<\varepsilon \text{ (Continuité de $f$ en $a$)} \\ \exists c\in \mathbb R, \forall \varepsilon>0, \exists \eta >0, 0< |x-a| <\eta \Rightarrow \frac1{|x-a|}|f(x)-f(a)-c(x-a)|<\varepsilon \text{ (Dérivabilité de $f$ en $a$)} \end{align*} $$

En notant la distance $d$ au lieu de $|.|$, ça donne: $$ \begin{align*} \forall \varepsilon > 0,\ \exists \eta>0,\, d(x,a) <\eta \Rightarrow d(f(x),f(a))<\varepsilon \\ \exists c\in \mathbb R, \forall \varepsilon>0, \exists \eta >0, 0< d(x,a) <\eta \Rightarrow \frac1{d(x,a)}d(f(x),(f(a)+c(x-a))<\varepsilon \end{align*} $$

Donc, dans $\mathbb R^n$, si on savait calculer la distance $d$ entre deux points, on pourrait recycler les mêmes définitions.

Et pour cela, il suffit de savoir calculer la longueur $N(\vec x)$ d'un vecteur $\vec x\in \mathbb R^n$. De là, la distance entre deux points, c'est la longueur de la différence des vecteurs correspondants: $d(\vec x, \vec y)= N(\vec x - \vec y)$.

Normes sur $\mathbb R^n$

Il se trouve qu'il y a de nombreuses façons de calculer la longueur d'un vecteur de $\mathbb R^n$: on appelle cela une norme sur $\mathbb R^n$.

Définition générale d'une norme

Il y a la norme euclidienne $N_2(\vec x)=\sqrt{x_1^2+...+x_n^2}$ qui généralise la distance usuelle sur $\mathbb R^2$ avec laquelle on travaille en géométrie. Mais ce n'est pas la seule: par exemple, $$ N(\vec x)= 3x_1^2 + \frac1{\pi} |x_2|+48\sqrt{3} |x_3| $$ en est une autre.

Heureusement, toutes ces façons de calculer la longueur d'un vecteur sont "équivalentes": si on fait de l'analyse avec l'une de ces normes, les fonctions continues, dérivables, etc. qu'on obtiendra seront les mêmes que pour toutes les autres normes.

Un complément à ce sujet par ici.

Boules dans $(\mathbb R^n, N)$

Une autre notion utile en analyse, liée à celle de distance, est celle d'intervalle. Un intervalle ouvert $]a,b[$ peut se réécrire $]m-r,m+r[$, où $m=\frac{a+b}2$ et $r=\frac{b-a}2$: c'est l'ensemble de tous les points de $\mathbb R$ dont la distance à $m$ est inférieure à $h$.

La notion équivalente dans $\mathbb R^n$, muni d'une norme $N$, est celle de boule: si $\vec m \in \mathbb R^n$ et $r>0$, $$ B(\vec m, r)=\{\vec x \in \mathbb R^n, N(\vec m, \vec x)< r\} $$

Mais le nom est trompeur: selon l'expression de $N$, les boules ne seront pas forcément rondes...

Voir ici les boules pour les normes $\|.\|_1,\|.\|_2,\|.\|_{\infty}$ dans $\mathbb R^2$.

Un programme pour visualiser d'autres normes est disponible ici.

Instructions: Pour les utiliser, allez dans le menu "Cell" et cliquez sur "Run All". Puis remontez en haut de la page.
Le temps de chargement peut être un peu long !